Bocoran Soal UTBK SNBT 2024 (Kunci Jawaban + Pembahasan)

Hallo Sobat 1Sekolahers, apakah kalian sudah siap untuk utbk 2024? UTBK-SNBT 2024 yang sudah tidak lama lagi. Ini akan menjadi salah satu jalan bagi mahasiwa untuk masuk ke perguruan tinggi negri melalui seleksi tes.Untuk melengkapi aktifitas belajar Sobat 1Sekolahers hari ini bakal ada soal dan pembahasan yang bisa untuk kamu jadikan bahan belajar.
Pada soal ini kita bakal mengulas soal dengan subtes PK (Pengetahuan kuantitatif). PK ini sendiri adalah soal yang berfokus ke mata pelajar matematika dengan materi Aljabar, Geometri, Pengukuran, Data dan statistik, dll.
Soal PK UTBK 2024
Soal No 1. Bilangan berikut yang habis dibagi 3, tetapi tidak habis dibagi 5 adalah...
Lihat Jawaban
Jawaban: B
Ciri bilangan yang habis dibagi tiga adalah jumlah angka pembentuknya merupakan kelipatan 3.
Ciri bilangan yang habis dibagi 5 adalah angka satuannya 0 atau 5.
12345: habis dibagi 3 dan habis dibagi 5 (S).
13689: habis dibagi 3, tetapi tidak habis dibagi 5 (B).
14670: habis dibagi 3 dan habis dibagi 5 (S).
15223: tidak habis dibagi 3 dan tidak habis dibagi 5 (S)..
20579: tidak habis dibagi 3 dan tidak habis dibagi 5 (S).
Soal No 2. Kurva y=ax²+2x+1 dengan a ≠ 0 memotong sumbu-x di dua titik berbeda. Pernyataan yang benar adalah...
Lihat Jawaban
Jawaban: A
Jika kurva y=ax²+2x+1 dengan a ≠ 0 memotong sumbu-x di dua titik berbeda, maka 2²-4a(1) > 0, sehingga a < 1
Soal No 3. Kurva y = ax² + 2x + 1 dengan a ≠ 0 memotong sumbu-x di dua titik berbeda. Pernyataan yang benar adalah...
Lihat Jawaban
Jawaban: C
Karena a<1 (berdasarkan soal nomor 2), a bisa positif atau negatif sehingga kurva bisa terbuka ke atas atau ke bawah, serta titik puncak kurva tidak harus di kuadran I.
Jika x=0, diperoleh y=1 sehingga kurva memotong sumbu- y positif.
Soal No 4. Garis dengan persamaan mana saja yang memotong garis 2x + y = 4 dan x + 2y = 2 di dua titik berbeda?...
1. y=-x+5
2. y=x-2
3. y = 3x-1
4. y=-2x+
Lihat Jawaban
Jawaban: B
Gradien garis 1 tidak sama dengan gradien garis 2 sehingga garis ketiga memotong dua garis tersebut di dua titik berbeda jika:
(a) gradiennya berbeda dengan kedua gradien garis yang lain, dan
(b) tidak melalui titik potong dua garis yang lain.
Oleh karena itu, garis dengan persamaan (1) atau persamaan (3) memotong dua garis lainnya di dua titik berbeda.
Soal No 5. Diberikan kumpulan data 3,5,7, a.
Berapakah banyaknya dari empat pernyataan berikut yang bernilai benar berdasarkan Informasi di atas?
1. Rata-rata kumpulan data tersebut 6 bila a=9
2. Median kumpulan data tersebut 5 bila a=7
3. Jangkauan kumpulan data tersebut 4 bila a=6.
4. Modus kumpulan data tersebut 3 bila a=5
A. 0
B. 1
C. 2
D. 3
E. 4
Lihat Jawaban
Jawaban: C
Untuk menentukan jumlah pernyataan yang benar, kita akan mengevaluasi setiap pernyataan berdasarkan informasi yang diberikan.
1. Rata-rata kumpulan data tersebut 6 bila a=9. =9.(3+5+7+9 /4 = 24/4 = 6 Pernyataan ini benar.
2. Median kumpulan data tersebut 5 bila a=7 . Urutan data: 3, 5, 7, 7 Median = (5+7)/2=6 Pernyataan ini salah.
3. Jangkauan kumpulan data tersebut 4 bila a=6. Urutan data: 3, 5, 6, 7 Jangkauan = nilai tertinggi nilai terendah = 7-34 Pernyataan ini benar.
4. Modus kumpulan data tersebut 3 bila a=5 Urutan data: 3, 5, 5, 7 Modus = 5 (karena muncul lebih dari satu kali) Pernyataan ini salah.
Dari keempat pernyataan, 2 pernyataan benar (pernyataan 1 dan 3). Jadi, jawabannya adalah C. 2.
Soal No 6. Tiga bola diambil dari sebuah kotak yang berisi 3 bola merah dan 2 bola putih. Misalkan B menyatakan kejadian terambilnya 2 bola merah dan 1 bola putih dan P(B) menyatakan peluang kejadian B.
Berdasarkan informasi yang diberikan, manakah hubungan antara kuantitas P dan Q berikut yang benar?
| P | Q |
|---|---|
| P(B) | 3/10 |
Lihat Jawaban
Jawaban: A
Peluang terambilnya 2 bola merah dan 1 bola putih adalah...
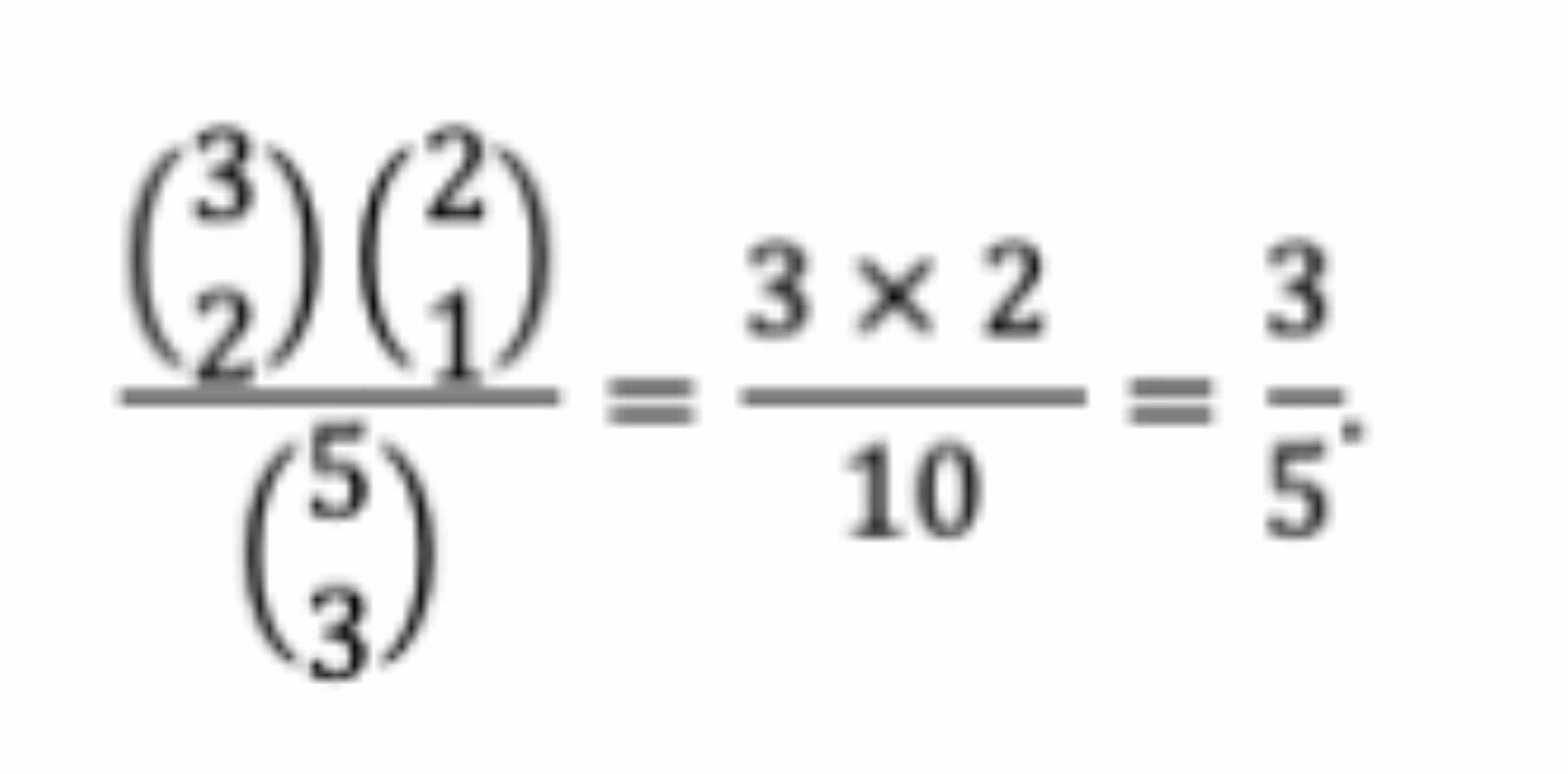
Soal No 7. Bilangan real x memenuhi pertidaksamaan 2x+1<4.
Berdasarkan informasi yang diberikan, manakah hubungan antara kuantitas P dan Q berikut yang benar?
| P | Q |
|---|---|
| -2x | 2 |
Lihat Jawaban
Jawaban: D
2x+142x32x > -3
Oleh karena itu, -2x bisa lebih dari atau kurang dari atau sama dengan 2 sehingga tidak dapat ditentukan hubungan antara kuantitas P dan Q.
Kesimpulan
Itulah contoh soal subtes penalaran kuantitatif untuk soal utbk 2024 nanti. semoga bermanfaat dan dapat meningkatkan kemampuan belajar kamu untuk persiapan utbk 2024 nanti.


Posting Komentar